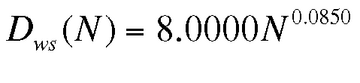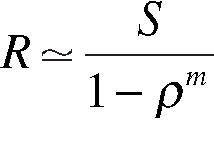Versteckte Latenzen berücksichtigen

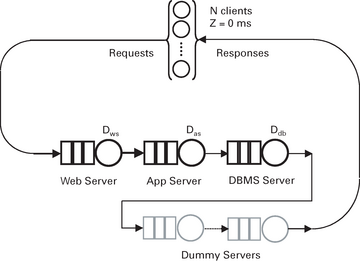
Als nächsten Trick fügt man dem PDQ-Modell aus Abbildung 11 Dummy-Knoten hinzu. Allerdings gibt es Bedingungen, die von den Bedienanforderungen der virtuellen Knoten zu erfüllen sind. Die Bedienanforderung eines jeden Dummy-Knotens ist so zu wählen, dass sie die Bedienanforderung des Engpassknotens nicht übersteigt. Darüber hinaus ist die Anzahl der Dummy-Knoten so zu wählen, dass die Summe der Serviceanforderungen einen Wert von Rmin = R(1) nicht übersteigt, sofern keine Konkurrenz auftritt, das heißt für eine Einzelanforderung. Wie sich herausstellt, lassen sich diese Bedingungen erfüllen, wenn man zwölf einheitliche Dummy-Knoten einführt, von denen jeder eine Serviceanforderung von 2,2 ms aufweist. Die Änderungen des entsprechenden PDQ-Codes sehen folgendermaßen aus:

Abbildung 11: Dummy-Knoten bilden versteckte Latenzen ab.

use constant MAXDUMMIES => 12;
$think = 0.0 * 1e-3; #same as in test rig
$dtime = 2.2 * 1e-3; #dummy service time
# Dummy-Knoten mit Bedienzeiten erstellen
for ($i = 0; $i < MAXDUMMIES; $i++) {
$dnode = "Dummy" . ($i < 10 ? "0$i" :U
"$i");
$pdq::nodes = pdq::CreateNode($dnode,U
$pdq::CEN, $pdq::FCFS);
pdq::SetDemand($dnode, $work, $dtime);
}

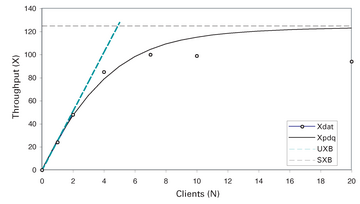
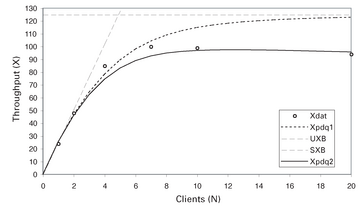
Man beachte, dass die Bedenkzeit wieder auf null zurückgesetzt ist. Die Ergebnisse dieser Änderungen am PDQ-Modell finden sich in Abbildung 12. Das Durchsatzprofil ist immer noch für geringe Lasten (N < N*) passend, wobei gilt

(13)

Abbildung 12: Durchsatz bei Z = 0 mit Dummy-Knoten.

Bestimmte Aspekte des physikalischen Systems wurden nicht gemessen, sodass die Validierung des PDQ-Modells schwerfällt. Bisher haben wir versucht, die Intensität der Arbeitslast durch Einführung einer positiven Bedenkzeit anzupassen. Die Einstellung von Z = 0.028 Sekunden beseitigte das Problem der schnellen Sättigung; gleichzeitig stimmt der Wert nicht mit dem Wert von Z = 0 Sekunden überein, der für die eigentlichen Messungen eingestellt wurde. Durch die Einführung von Dummy-Warteschlangenknoten ins  PDQ-Modell wurde das Modell für Szenarien mit geringer Last verbessert, aber dadurch wird dem in den Daten beobachteten Abfall des Durchsatzes nicht Rechnung getragen. Um diesen Effekt nachzubilden, können wir den Webserverknoten durch einen lastabhängigen Knoten ersetzen. Die Theorie der lastabhängigen Server wird in [5] besprochen.

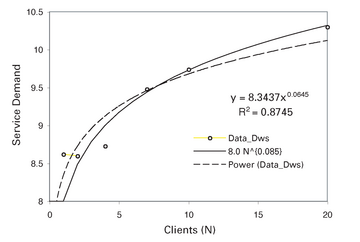
In unserem Beispiel wenden wir einen etwas einfacheren Ansatz an. Aus der Bedienzeit (Sws) in Tabelle 4 erkennt man, dass sie nicht für alle Clientlasten konstant bleibt. Es wird also eine Methode benötigt, um diese Variabilität auszudrücken. Wenn man ein Diagramm der Messdaten für Sws erstellt, lässt sich eine statistische Regressionsanpassung durchführen, wie sie Abbildung 13 zeigt. Die sich daraus ergebende Potenzgesetzgleichung lautet:

Abbildung 13: Regressionsanpassung der Webserver-Zeiten.

(14)

Damit wird Node1 des PDQ-Modells wie folgt parametrisiert:

pdq::SetDemand($node1, $work, $$
8.0 * 1e-3 * ($users ** 0.085));

Die angepasste Ausgabe des fertigen PDQ-Modells zeigt Tabelle 5. Sie zeugt von einer guten Übereinstimmung mit den gemessenen Daten für D = 12 Dummy-PDQ-Knoten.

Die Auswirkung auf das Durchsatzmodell lässt sich in Abbildung 14 erkennen. Die mit Xpdq2 gekennzeichnete Kurve zeigt den vorhergesagten übersteuerten Durchsatz auf Basis des lastabhängigen Servers für das Webfrontend, und die Vorhersagen liegen locker innerhalb des Fehlerbereichs der gemessenen Daten. In diesem Fall bringt es wenig, PDQ für die Vorhersage einer Last einzusetzen, die oberhalb der gemessenen Last von N = 20 Clients liegt, weil der Durchsatz nicht nur gesättigt ist, sondern auch rückgängig. Nachdem nun ein PDQ-Modell existiert, das mit den Testdaten validiert wurde, kann man jetzt alle erdenklichen Was-wäre-wenn-Szenarien durchspielen.

Abbildung 14: Modell des lastabhängigen Durchsatzes.

Das vorherige Beispiel ist bereits ziemlich anspruchsvoll, und ähnliche PDQ-Modelle sind für die meisten Anwendungsfälle vollkommen ausreichend. Allerdings gibt es auch Situationen, in denen detailliertere Modelle erforderlich sein können. Zwei Beispiele für diese Szenarien sind multiple Server und multiple Aufgaben.

Multiple Server

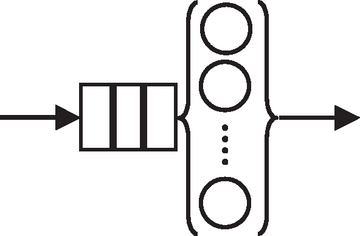
Ein Szenario außerhalb der Computerwelt, das man mithilfe der Warteschlange mit multiplen Servern aus Abbildung 15 nachbilden könnte, ist das Schlangestehen in einer Bank oder einem Postamt. Im Kontext der Computer-Performance könnte Abbildung 15 als einfaches Modell eines symmetrischen Mehrprozessorsystems dienen.

Abbildung 15: PDQ-Modell einer Multiserver-Warteschlange.

Weitere Informationen zu diesem Thema finden Sie in Kapitel 7 von [5]. Die Antwortzeit in (1) wird durch Folgendes ersetzt:

(15)

wobei r = lS, und m ist die integrale Anzahl von Servern. Technisch betrachtet handelt es sich um eine Annäherung, aber keine schlechte! Die genaue Lösung ist komplexer und lässt sich mit dem folgenden Perl-Algorithmus entdecken (Listing 4).

Es handelt sich um genau das Warteschlangenmodell, das Erlang vor 100 Jahren entwickelt hat. Damals stellte jeder Server eine Hauptleitung im Telefonnetz dar.